Art of Problem Solving Number of Permutations 1 Belongs to a Cycle
Permutations
Definition 1.10
- A permutation of a set X is a bijection from X to X.
- If \(X=\{1,2,\ldots,n\}\) we write \(S_n\) for the set of all permutations of X, and call \(S_n\) the symmetric grouping on n messages.
Sometimes, like when \(X=\{ane,2,three,\ldots,n\}\), a ready comes with a natural order. Then a permutation \(\sigma\) can be idea of equally a re-ordering of X, since the elements \(\sigma(one),\sigma(2),\ldots,\sigma(n)\) are the numbers 1,2,…,n written in some different order.
If \(\sigma\) and \(\tau\) are permutations nosotros will oft write \(\sigma \circ \tau\) every bit \(\sigma \tau\), and refer to information technology as the product of \(\sigma\) and \(\tau\) instead of the composition.
2 row annotation
To record an element \(\sigma\in S_n\), we need to say what \(\sigma(i)\) is for \(ane\leq i \leq n\). One way to exercise this is two row notation in which nosotros write the numbers ane to n in a row so write \(\sigma(i)\) beneath i: \[ \begin{pmatrix} ane & 2 & \cdots & n-1 & north \\ \sigma(one) & \sigma(2) & \cdots & \sigma(northward-1) & \sigma(n) \end{pmatrix} \] Because elements of \(S_n\) are bijections, the numbers actualization on the bottom row are but i,ii,…,n written in a possibly different order.
The inverse of a bijection is again a bijection so if \(\sigma \in S_n\) then \(\sigma^{-ane} \in S_n\). If we have \(\sigma\) in two row notation it is piece of cake to find its inverse: since \(\sigma^{-1}\) must send \(\sigma(i)\) to i, nosotros only swap the two rows and then rearrange the columns then that the top row is in the correct order. For instance, if we begin with \[ \sigma = \begin{pmatrix} 1 & 2 & iii & 4 & 5 \\ 3 & 4 & v & 1 & 2 \end{pmatrix} \] and then on swapping the rows nosotros get \[ \brainstorm{pmatrix} three & 4 & 5 & 1 & 2 \\ 1 & 2 & 3 & four & five \end{pmatrix} \] and rearranging gives \[ \sigma^{-ane} = \begin{pmatrix} i & 2 & three & 4 & v \\ 4 & five & ane & 2 & 3 \end{pmatrix}.\]
Theorem 1.three \(|S_n|=n!\).
Proof. Induction on n. When \(northward=1\) at that place is a unique bijection \(\{one\}\to\{i\}\), namely the identity map, and then \(|S_1|=1=1!\) equally required.
For the inductive step, annotation that the number of elements of \(S_n\) is the number of different ways to order the elements \(one,two,\ldots,northward\). An ordering of \(1,2,\ldots,n\) is the aforementioned thing every bit an ordering of \(i,2,\ldots,northward-1\) with n inserted into one of north positions, and so the number of possible orderings is n times the number of orderings of \(i,\ldots,due north-1\), which is \((n-1)!\) by the inductive hypothesis. So \(|S_n|=n\times (north-ane)!=n!\), completing the inductive step.
Cycles
Definition 1.xi
- Permit \(a_0,\ldots,a_{m-1}\) exist distinct elements of \(\{one,2,\ldots,n\}\). And then \((a_0,\ldots,a_{grand-1})\) is the permutation in \(S_n\) such that \(a_i \mapsto a_{i+1}\) for \(0\leq i < m-i\), \(a_{m-1}\mapsto a_0\), and if \(x \neq a_1,\ldots,a_m\) then \(ten \mapsto x\). Such a permutation is called an thousand-wheel
- A permutation which is an thou-cycle for some g is called a wheel.
- Ii cycles \((a_0,\ldots,a_{1000-ane})\) and \((b_0,\ldots,b_{fifty-1})\) are called disjoint if no \(a_i\) is equal to whatsoever \(b_j\).
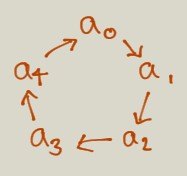
Figure 1.7: Illustration of a 5-bicycle. \(a_0,a_1,a_2,a_3,a_4\) are shown in a circle with an arrow pointing from i to the next, and then from \(a_4\) back to \(a_0\)
Not every permutation is a cycle, e.g. \[ \brainstorm{pmatrix} 1&ii&three&4\\ 2&1&4&3 \end{pmatrix}. \] On the other hand, as nosotros will prove in this section, whatever permutation can exist written as a product of disjoint cycles: y'all can check that the permutation above is equal to \((one,2)(3,4)\). To give the proof, nosotros need some farther ideas related to permutations. Commencement we are going to define powers of permuations in such a way that the usual exponent laws apply.
Definition one.12 Permit \(chiliad\in\mathbb{Z}\) and \(\sigma\in S_n\). Then \[ \sigma^yard = \brainstorm{cases} \sigma \circ \cdots \circ \sigma \;\; (m \text{ times}) & g>0 \\ \id & 1000=0 \\ \sigma^{-1}\circ \cdots \circ \sigma^{-one} \;\; (-m \text{ times}) & 1000<0 \end{cases} \]
It's slightly tedious, but you tin check that for any \(a,b\in\mathbb{Z}\) we have \[ \sigma^a \sigma^b = \sigma^{a+b}.\] There is a proof of a more general effect in the section of these notes on groups.
Definition 1.thirteen Let \(ten \in \{1,ii,\ldots,n\}\) and \(\sigma \in S_n\). The orbit of 10 under \(\sigma\), written \(\operatorname{orb}(ten)\), is \[ \operatorname{orb}(x) = \{\sigma^1000(x) : grand \in \mathbb{Z}\} .\]
Despite appearances, \(\operatorname{orb}(ten)\) is a finite set because it is a subset of \(\{one,\ldots,n\}\). We tin can say a little about what \(\operatorname{orb}(ten)\) looks like using the following outcome:
Suggestion 1.4 Let \(x \in \{ane,\ldots,n\}\) and \(\sigma \in S_n\). Then there is a whole number \(r>0\) such that \(\sigma^r(x)=x\).
Proof. The elements \(\sigma^m(x)\) for \(m=0,1,two,\ldots\) can't all be unlike, so there must exist \(i<j\) such that \(\sigma^i(ten)=\sigma^j(x)\). Then \(\sigma^{-i}\sigma^i (x) = \sigma^{-i}\sigma^j (x)\), so \(10 =\sigma^{j-i}(x)\) and nosotros can take \(r=j-i\).
Finally nosotros're fix to describe the orbit of x:
Proposition i.5 Let \(\sigma\in S_n\) and \(x \in \{i,2,\ldots,due north\}\), and let r be the smallest strictly positive natural number such that \(\sigma^r(x)=10\). Then
- \(\orb(x)=\{x, \sigma(10), \ldots, \sigma^{r-one}(x)\}\), and
- all of the elements \(x,\sigma(x),\ldots,\sigma^{r-one}(ten)\) are different.
Discover that we needed the proposition before this to establish that such an r exists.
Proof.
- Let \(\sigma^a \in \orb(ten)\), we have to show that it equals one of \(x, \sigma (x), \ldots, \sigma^{r-1}(x)\). To do that, write \(a=qr+b\) where b is the rest on dividing a by r, so that \(0 \leq b < r\). Then \(\sigma^a(x)= \sigma^{qr+b}(10) = \sigma^b( \sigma^{rq}(x))\). Simply \(\sigma^r(x)=ten\), so \(\sigma\) to the power of whatever multiple of r sends x to itself as well. Thus \(\sigma^a(x) = \sigma^b(x) \in \{10,\sigma(x),\ldots,\sigma^{r-ane}(10)\}\).
- If \(\sigma^i(ten)=\sigma^j(x)\) for some \(ane\leq i<j<r\) and then \(10=\sigma^{j-i}(ten)\) equally before, and \(0<j-i<r\) which contradicts r existence the smallest strictly positive natural number with \(\sigma^r(ten)=10\).
This really gives a way of calculating orbits: if we want \(\orb(ten)\) nosotros just find \(10, \sigma(10), \sigma^2(ten),\) and and so on, stopping when we showtime get back to x. The terminal proffer guarantees that this listing is the complete orbit of x with no repetitions.
Proposition ane.6 Allow \(\sigma \in S_n\). Define a relation \(\sim\) on \(\{ane,2,\ldots,north\}\) past \(ten\sim y\) if and only if \(10 \in \orb(y)\). And so \(\sim\) is an equivalence relation and the equivalence classes are the orbits of \(\sigma\).
Proof.
- (R): certainly \(ten \in \orb(x)\), so \(x\sim x\).
- (South): if \(x ~y\) and so \(10\in \orb(y)\), so \(x=\sigma^a(y)\) for some a, and then \(\sigma^{-a}(x) = \sigma^{-a}\sigma^a(y)=y\). Therefore \(y \in \orb(x)\), and \(y\sim ten\).
- (T): if \(10\sim y\sim z\) then \(x\in \orb(y)\), and so \(10=\sigma^a(y)\) for some a, and \(y \in \orb(z)\), and then \(y=\sigma^b(z)\) for some b. Then \(x=\sigma^a(\sigma^b(z))=\sigma^{a+b}(z) \in \orb(z)\), so \(10\sim z\). Since \(y\sim x\) if and only if \(y \in \orb(x)\), the equivalence class \([x]\) is \(\orb(x)\).
Theorem 1.iv Every chemical element of \(S_n\) tin can exist written every bit a product of disjoint cycles.
Proof. Let \(\sigma \in S_n\) and let the singled-out orbits of \(\sigma\) exist \(\orb(x_1),\ldots,\orb(x_m)\). These are the equivalence classes for an equivalence relation, then every element of \(\{1,2,\ldots, n\}\) belongs to exactly i of these orbits. Nosotros as well know that \[ \orb(x_i) = \{x_i, \sigma(x_i), \ldots , \sigma^{r_i-1}(x_i)\} \] where \(r_i\) is the smallest strictly positive natural number such that \(\sigma^{r_i}(x_i)=x_i\).
Let \(c_i\) be the cycle \((x_i, \sigma(x_i), \ldots, \sigma^{r_i-ane}(x_i))\), so that the \(c_i\)s are disjoint cycles because the orbits of \(\sigma\) are disjoint. We volition show that \[ \sigma = c_1 c_2 \cdots c_m \] To bear witness this nosotros demand to show that if j is any chemical element of \(\{1,ii,\ldots,n\}\) then the product of disjoint cycles on the correct sends j to \(\sigma(j)\). But this is true, considering in each bike \(c_i\) every chemical element \(\sigma^a(a_i)\) is sent to \(\sigma^{a+i}(x_i) = \sigma ( \sigma^a(a_i))\).
The theorem gives united states a way of expressing a given permutation as a production of disjoint cycles: beginning we observe the orbits, then each orbit gives rise to a cycle and the product of these cycles is equal to our original permutation.
Transpositions and the sign of a permutation
Definition ane.xiv A transposition is a 2-cycle.
Lemma one.2 If \(a_0, \ldots, a_{m-1}\) are distinct and then \[(a_0, a_1, \ldots, a_{k-1}) = (a_0,a_1)(a_1, a_2)\cdots (a_{m-2},a_{m-one})\]
Proof. Induction on m. For \(m=2\) there is cypher to prove. For the inductive step, we can presume that \((a_0,a_1)\cdots (a_{m-2}, a_{thou-1}) = (a_0,\ldots,a_{m-1})\) and we must show that if nosotros multiply this on the correct past \((a_{yard-i}, a_m)\) nosotros become \((a_0,\ldots,a_m)\).
Consider the permutation \[ (a_0,\ldots,a_{m-1})(a_{one thousand-1},a_m).\] Every number not an \(a_i\) is sent to itself by this permutation. Every \(a_i\) for \(i \leq m-2\) is sent to \(a_{i+1}\), since it is fixed past the 2-cycle. \(a_{m-1}\) is sent to \(a_m\) by the 2-cycle and this is stock-still past the one thousand-bicycle. \(a_m\) is sent to \(a_{k-1}\) by the ii-bicycle and then to \(a_0\) by the m-cycle. Summarizing, \(a_i\) goes to \(a_{i+i}\) for \(i<chiliad\) and \(a_m\) goes to \(a_0\), hence this permutation is the m+1 cycle \((a_0,\ldots,a_m)\).
Proposition 1.7 Every permutation is equal to a product of transpositions.
Proof. Let \(\sigma\) be any permutation. Theorem i.iv says we tin can limited \(\sigma\) equally a product of disjoint cycles. The previous lemma says we can express each of these cycles as a product of transpositions. This expresses \(\sigma\) as a product of transpositions.
Definition i.xv A permutation is fifty-fifty if it can be written as a production of an fifty-fifty number of transpositions, and odd if it can exist written equally an odd number of transpositions.
For case, the identity permutation \(\id = (ane,ii)(1,2)\) and then it is even. It follows straight from the definition that an even permutation multiplied by another even permutation is even, even times odd is odd, odd times even is odd, and odd times odd is even.
It's not clear even so that a permutation couldn't exist odd and even at the same fourth dimension.
Theorem i.5 Every permutation is either odd or even, only not both.
Proof. (Sketch). Commencement we know from the previous proposition that every permutation can be written as a product of transpositions, then the only problem is to testify that it is non possible to find two expressions for a given permutation, one using a production \(s_1 s_2 \cdots s_{2m+1}\) of an odd number of transpositions and one using a product \(t_1 t_2 \cdots t_{2l}\) of an even number of transpositions. The steps are as follows:
- If this were the instance and so nosotros would take \(\id = t_{2l}\cdots t_1 s_1 \cdots s_{2m+1}\), expressing the identity every bit a product of an odd number of transpositions, and then it is plenty to prove this impossible.
- Observe that whatsoever transposition \((i,j)\) can exist written \[ (j-ane,j)\cdots (i+2,i+3)(i+1,i+2) \times (i,i+1) \times (i+1,i+2)(i+ii,i+iii)\cdots (j-one,j)\] where we have causeless without loss of generality that \(i<j\). This is a product of an odd number of adjacent transpositions, i.eastward. transpositions of the form \((yard,k+i)\).
- So it is enough to show that the identity cannot be written as a product of an odd number of adjacent transpositions.
- Consider polynomials in the n variables \(x_1,\ldots,x_n\). If you lot have such a polynomial \(f(x_1,\ldots,x_n)\) and a permutation \(\sigma \in S_n\), you get a new polynomial \(\sigma(f)\) by replacing each \(x_i\) in f with \(x_{\sigma(i)}\). For case, if \(\sigma = (ane,ii,three)\) and \(f=x_1+x_2^2\) then \(\sigma(f)=x_2+x_3^2\). Define \[ \Delta = \prod_{1\leq i<j \leq due north}(x_i-x_j)\]
- Observe that for any chiliad, \((m,yard+1)(\Delta) = -\Delta\), and so whatever product of an odd number of adjacent transpositions sends \(\Delta\) to \(-\Delta\) too.
- Get a contradiction from the fact that \(\id(\Delta) = \Delta\).
Proffer 1.8
- The identity permutation is even.
- An m-cycle is even if m is odd and odd if yard is even.
Proof.
- \(\id = (1,2)(i,2)\).
- This follows from ane.2.
Definition ane.sixteen The sign of a permutation \(\sigma\), written \(\sgn(\sigma)\), is \[ \sgn(\sigma) = \brainstorm{cases} \phantom{-}1 & \sigma \text{ is even} \\ -1 & \sigma \text{ is odd.} \end{cases} \]
Thus \(\sgn (a_0,\ldots,a_{m-i}) = (-1)^{m-ane}\). Sign has a dainty property:
Proffer ane.9 For whatsoever permutations \(\sigma\) and \(\tau\) we have \(\sgn(\sigma \tau) = \sgn(\sigma)\sgn(\tau)\).
Proof. This is just a restatement of the fact that an even permutation composed with an even permutation is fifty-fifty, an odd permutation composed with an odd permutation is fifty-fifty, and an odd permutation equanimous with an even permutation is odd.
This lets us find the sign of an arbitrary permutation: starting time express information technology as a production of cycles (they don't have to be disjoint), then use this result and the fact that even length cycles are odd and odd length cycles are fifty-fifty.
Source: https://www.ucl.ac.uk/~ucahmto/0007/_book/1-4-permutations.html
0 Response to "Art of Problem Solving Number of Permutations 1 Belongs to a Cycle"
Post a Comment